Cube 2

Once upon a time, there was a man called Graham, and he was wondering about cubes. By the time he'd finished wondering, he'd come up with the largest numerical answer to a reasonable question* in the history of the world.

Here's the game. Draw a cube. Draw lines joining each corner to every other corner. Colour each line either blue or red, as you wish. Your cube might look like this:


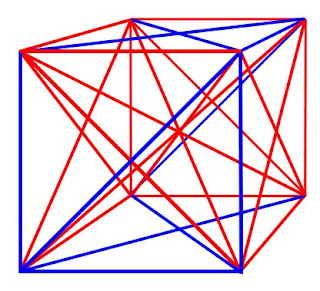
Now look and see if there are any red or blue ☒s in your cube.

Technically, we're looking for a single-coloured, planar K₄ graph. Which means a ☒.

In the picture above, in amongst the tangle of blue and red, there is one red ☒ and no blue ones. The red one looks like this:


(There will be twelve ☒s in a single-coloured 3D cube, so twelve possible places to find a red or blue ☒ in a bi-coloured cube.)

Now, can you make this cube into one that has no ☒? In this case, it's easy. Change any one of the red lines of the ☒ above to a blue line, and the cube will have no ☒s anywhere in it.

So it's easy to construct a 3D cube with no ☒s. Things get trickier when you look at cubes in more than three dimensions (sometimes called hypercubes). Ronald Graham and Bruce Rothschild, in 1971, found cubes in four and five dimensions having no ☒s. Six dimensions was too tricky at that time. However – and this gives an indication of the complexity of the problem – with modern computing, this has more recently been extended to ten-dimensional cubes... but no further.

What Graham and Rothschild wanted to know was this: if you make your cubes in ever higher dimensions, is it always possible to make a cube with no ☒s?

How they answered this, I can confidently state I will never know. Mathematics is a strange and beautiful world, full of many lands I'll never have either the will or the means to travel very far in. This particular land is known to devotees as Ramsey Theory, belonging to a branch of mathematics called Extremal Combinatorics, and I have come across some neat little problems to explore there. But if we're talking travelling, I never made it out of the airport. All I can say is that in 1971, the year of my birth, our explorers proved that the answer is no, it isn't. At some point, once you get to a certain number of dimensions, there will have to be a ☒somewhere in the cube: there is no way of making a bi-coloured cube in so many dimensions without it containing at least one ☒.

So what's the maximum number of dimensions for a cube with no ☒s? As yet, we don't know. Graham and Rothschild – as noted earlier – showed that it was at least six.

A few years later, Graham went on to prove that it's certainly no more than the number we now know as Graham's Number.

So it's got to be somewhere between those two.

What is Graham's Number? Well, it's big – rather too big to describe succinctly. The only way to get there is by a set of stages, and by introducing arrow notation (↑), so that is what I'll try to do here.

Graham's number is built up using lots and lots of the number 3.

One arrow: ↑ (exponentiation)
3↑3 is simply 3³ – that is, raise 3 to the power of 3. This is "3 times 3 times 3", which is 27.

Two arrows: ↑↑ (tetration)
3↑↑3 is "3 to the power of (3 to the power of 3)", or 3 to the power of 27, which is 7,625,597,484,987.
3↑↑4 is 3 to the power of 7,625,597,484,987 (already greater than the number of random monkey keystrokes required to reproduce the Complete Works of Shakespeare – or, for that matter, the entire contents of the Bodelian Library – in one burst), and 3↑↑5 is 3 to the power of that.
And so on.
(seven trillion steps later...)

Three arrows: ↑↑↑
3↑↑↑3 is 3↑↑(3↑↑3), which is: "3 to the power of (3 to the power of (3 to the power of (3 to the power of ... (3 to the power of 3)...)))". The dots signify the omission of repeated elements such that, if written fully, the number 3 would appear 7,625,597,484,987 times here.

3↑↑↑4 is 3↑↑(3↑↑(3↑↑3)) – as above, but the number 3 would appear 3↑↑↑3 times instead.

3↑↑↑5 is 3↑↑(3↑↑(3↑↑(3↑↑3))) – as above, with the number 3 appearing 3↑↑↑4 times.

Continuing in this way we get 3↑↑↑6, 3↑↑↑7... and eventually, after 3↑↑↑3 such steps, we get to 3↑↑↑(3↑↑↑3).

Four arrows: ↑↑↑↑
3↑↑↑↑3 is 3↑↑↑(3↑↑↑3)
And this, 3↑↑↑↑3, is the starting point for Graham's Number. We call this g₁
g₁ = 3↑↑↑↑3.

We could plough on like this to get to five arrows – obviously this would be an even more vast set of steps up for our number. But we have to move a lot faster than this, otherwise we'll never get there.

So imagine not five, not six, but g₁ arrows...

3↑↑↑↑3 arrows
g₂ = 3↑↑↑...{g₁ arrows}...↑↑↑3.

Even more arrows!
If we use g₂ arrows, we get g₃.
If we use g₃ arrows, we get g₄.

And so on, another sixty times... until we arrive at:

g₆₄= 3↑↑↑...{g₆₃ arrows}...↑↑↑3.

And that's Graham's number.

A cube in this number of dimensions would have 2^g₆₄ corners. And each one joined to every other one, so square that and divide by two, and you have a lot of blue and red lines. Graham proved that there would definitely be a ☒ in there somewhere.

So, returning to the question: what's the maximum number of dimensions for a cube with no ☒s? The answer was "well, it's at least six, but not more than Graham's Number". This must be the least precise answer in the history of mathematics. And the 21st Century update – using computers to narrow of the range to "well, it's at least eleven, but not more than Graham's Number" – doesn't, on the face of it, make it a great deal better.

The thing is, there's something magical about the unsolved problems in mathematics and the quest for their solutions – especially the ones that are on the edge of solubility like this one. The efforts of those attempting to solve the problem thus far might seem fruitless. Indeed, it might be hard to imagine what the point would be even if the answer to our question were ever found. But for anyone who's ever allowed themselves to be fascinated by these things, they soon quite naturally appear as ends in themselves. Their point is in their own poetry, their own mystery, which the application of precision, logic and reason only magnifies.

This particular question can be re-stated in terms of sets of people joining committees, rather than bi-coloured hypercubes. It might also be related to computing (as I alluded to here). Who knows what use it might turn out to have. I'm not sure I could care less about its uses. The purpose is in the thing itself, on its own terms and in its own world. In the sensing, by whatever peculiar human faculty allows it, of the fantastic nature of these worlds – and in the marvelling at the minds of the peculiarly eccentric beings who explore them.

*by a 'reasonable question', what I really mean is a question that makes sense without being framed in terms of incomprehensibly large numbers. So, no, "what's Graham's number plus one?" doesn't count...