Today: something cubish. Bear with me on this one.
1D: If you have a little line, you can use it to represent any 'bipolar' situation, like the potential outcomes of tossing a coin. You could label the ends H and T, or, if you like a spot of binary, 0 and 1.
2D: If you have a square, the four corners could represent the possible outcomes of tossing two coins (HH, HT, TH, TT). You might label them 00, 01, 10, and 11.

3D: A cube has eight corners (000,001,010,011,100,101,110,111). Looked at in a certain way, it's a map of the eight possible states of a three-bit computer. You could use this computer to store the result of three coin tosses, or perhaps a letter from a to h. At any one time, your computer would inhabit one corner of the cube. The cube is its little world of potential: if you give it a different letter to store, or a different set of coin toss results, it moves to a different corner of its world.
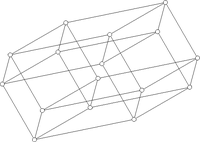
4D: A 'hypercube', has 16 corners. (If you're curious about cubes in four dimensions, there's a lovely explanation
here - scroll down to 'Analogies to Lower Dimensions' and enjoy.) A computer living here would have four bits - a semibyte.
The laptop I'm typing into has a modest 80GB of storage, which is about 687 billion bits. It lives in a 687 billion-dimensional cube, flitting from corner to corner like a fly in a box. Every stroke of the key sends it to another corner. Even when I stop, it flits through dimensions I'm not aware of. I can hear it. Flitting.
One can't help feeling pity for the poor thing...
And it was between such bouts of pity that I took to wondering what it might be like in 687 billion dimensions (invariably a good move if at any time you find yourself fed up of any form of compassionate state).
A spot of Pythagoras (or a quick sketch with a ruler) will tell you that the diagonal of a 1cm square is about 1.4cm long. The equivalent distance for a 1cm cube - in a straight line between opposite corners - just over 1.7cm.
If you're ever trapped inside a 1cm crouton, or a sugar cube, you'll always be able to stretch out to 1.7cm long if you need to.
Picture now a sugar cube in 687 billion dimensions, still just 1cm across. The distance between opposite corners? A little over 5 miles.
This exercise has helped me come to terms with the plight of my flitting friend; and maybe it can help you too. No more fly in a box visions for me. I see my sweet laptop soar on snow-white wings through miles of sparkling space, to liquid crystal heights and diaphanous digital depths, and I am at peace.

 Yesterday I had a day out at the Natural History Museum, including one of the most quietly thrilling exhibitions I've ever seen.
Yesterday I had a day out at the Natural History Museum, including one of the most quietly thrilling exhibitions I've ever seen.  Yesterday I had a day out at the Natural History Museum, including one of the most quietly thrilling exhibitions I've ever seen.
Yesterday I had a day out at the Natural History Museum, including one of the most quietly thrilling exhibitions I've ever seen.  3D: A cube has eight corners (000,001,010,011,100,101,110,111). Looked at in a certain way, it's a map of the eight possible states of a three-bit computer. You could use this computer to store the result of three coin tosses, or perhaps a letter from a to h. At any one time, your computer would inhabit one corner of the cube. The cube is its little world of potential: if you give it a different letter to store, or a different set of coin toss results, it moves to a different corner of its world.
3D: A cube has eight corners (000,001,010,011,100,101,110,111). Looked at in a certain way, it's a map of the eight possible states of a three-bit computer. You could use this computer to store the result of three coin tosses, or perhaps a letter from a to h. At any one time, your computer would inhabit one corner of the cube. The cube is its little world of potential: if you give it a different letter to store, or a different set of coin toss results, it moves to a different corner of its world. 4D: A 'hypercube', has 16 corners. (If you're curious about cubes in four dimensions, there's a lovely explanation here - scroll down to 'Analogies to Lower Dimensions' and enjoy.) A computer living here would have four bits - a semibyte.
4D: A 'hypercube', has 16 corners. (If you're curious about cubes in four dimensions, there's a lovely explanation here - scroll down to 'Analogies to Lower Dimensions' and enjoy.) A computer living here would have four bits - a semibyte.
 They have complex lives.
They have complex lives.